Merkelized List¶
Merkelized list is a version of a typed list that supports compact proofs of existence for its elements using Merkle trees. Merkelized lists in Exonum are designed as classic binary Merkle trees within the persistence module, but can also be viewed as append-only lists by client and service developers.
A Merkle tree (aka hash tree or Tiger tree hash) is a tree in which every non-leaf node is labelled with the hash of the labels or values (in case of leaves) of its child nodes. Hash trees are a generalization of hash lists and chains. Merkle trees include both benefits of
- Trees: operations on elements (appending a new element, getting an
element) take
O(log N)operations, whereNis number of elements (for example, transactions) - Hashes: verification of the (blockchain) copies.
Motivation and Usage¶
In the blockchain as in various other distributed and peer-to-peer systems, data verification is very important because the same data exists in multiple locations. Thus, if a piece of data is changed in one location, it is important that the same data changes are processed everywhere in the same way.
It is time consuming and computationally expensive to check the entirety of each part whenever a system wants to verify data. This is why Merkle trees are used. Basically, the use of Merkle trees limits the amount of data being sent over a network as much as possible. Instead of sending an entire file over the network, it is possible just send a hash of the file to see if it matches.
Currently, the main uses of Merkle trees are in peer-to-peer networks such as Tor and Bitcoin. The usage of Merkle tree for blockchains (including Bitcoin and Exonum) is twofold:
- Minimization of the data transfer during the blockchain state agreement during Precommit phase of the consensus algorithm
- Possibility of light clients implementation.
ProofListIndex Storage Specification¶
Operator || below stands for concatenation. Function hash(arg) below
stands for SHA-256 hash of byte array arg.
Persistence¶
The internal representation of a Merkle tree is organized by utilizing 2 integer
parameters as a key for each element: height and index.
Note
To distinguish values from different lists in Exonum, an additional prefix is used for every key. Consult MerkleDB for more details.
Each Merkle tree element is addressed by an 8-byte key = height || index,
where:
height <= 56is height of element in the tree, whereheight = 0denotes a leaf.heightis represented as 8 bits (i.e., 1 byte)indexis index of element at the given height consisting of the other 56 bits (7 bytes)indexare serialized withinkeyas big-endian values
Note
This storage design means that the maximum supported number of elements
in a ProofListIndex is 2 ** 56 (approximately 7.2e16),
rather than 2 ** 64. We consider this amount sufficient
for practical applications.
The elements of the underlying list are stored in (height = 0, index)
cells, where index is in interval [0, list.len()) and
list.len() is the number of leaves in the tree (or, equivalently, the
number of elements in the underlying list).
Hash of a tree leaf is stored in (height = 1, index).
It corresponds to the tree leaf stored in (height = 0, index).
Some of the rightmost intermediate nodes may have a single child; it is not
required that the obtained tree is full binary. Appending an element to the
list corresponds to writing it to the cell (0, list.len()) and updating
O(log list.len()) nodes of the tree with height > 0.
A node at (height > 1, index) stores hashes of 1 or 2 child nodes.
- If both
(height - 1, index * 2)and(height - 1, index * 2 + 1)nodes are present, the node(height, index)has 2 children hashes. - If only
(height - 1, index * 2)node is present, the node at(height, index)has single child hash.
max_height is the minimal height at which only a single hash is stored at
index = 0.
max_height = pow + 1, wherepowis the smallest integer such that2^pow >= list.len()(max_height, 0)defines the root hash of the Merkle tree.
An example of key–value mappings in database:
| Key | Height | Index | Value |
|---|---|---|---|
| 00 00 00 00 00 00 00 FF | 0 | 255 | serialized value |
| 04 00 00 00 00 00 00 05 | 1 | 5 | hash |
| 0C 00 00 00 00 00 00 0A | 3 | 10 | hash |
Logical Representation¶
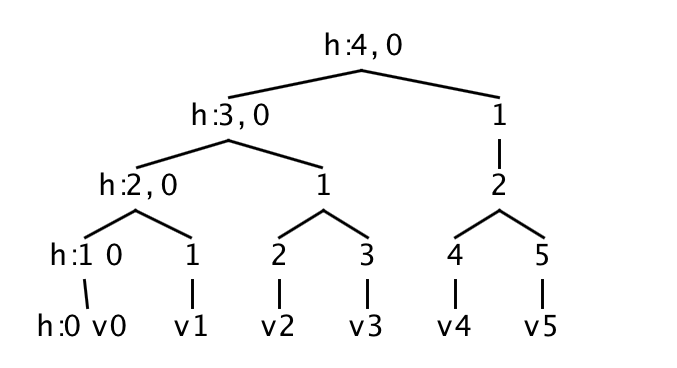
Below is an illustration of the logical representation of a Merkle tree,
containing 6 values v0...v5:
Computing List Hash¶
Hashing a Merkelized list consists of two logical operations:
- Computing the root hash of the tree
- Computing the list hash using the root hash and the list length.
Since the second component is easier, we will define it first.
Given the list length len and the root_hash of a Merkle tree corresponding
to the list, the list hash is defined as
h = sha-256( HashTag::ListNode || u64_LE(len) || root_hash )
Here,
HashTag::ListNode = 2is a tag separating lists from other hashed objects. (Here and elsewhere, tags are serialized as a single byte.)u64_LEis an 8-byte little-endian serialization of an integer.
Computing Root Hash¶
Let T(height, index) be a value at tree node for element index at height
height. Elements T(0, index) contain serialized values of the underlying list.
Elements T(height, index) for height > 0 are hashes corresponding the following
rules.
Rule 1. Empty Tree¶
Root hash of an empty tree is defined as 32 zero bytes.
Rule 2. Bottommost Hashes¶
Hash of a value contained in (height = 0, index) is defined as
T(1, index) = hash(HashTag::Blob || T(0, index)),
where HashTag::Blob = 0 is a domain separation tag for values.
Rule 3. Nodes with Two Children¶
If height > 1 and both nodes T(height - 1, index * 2) and
T(height - 1, index * 2 + 1) exist, then
T(height, index) = hash(
HashTag::ListBranchNode ||
T(height - 1, index * 2) ||
T(height - 1, index * 2 + 1)
),
where HashTag::ListBranchNode = 1 is a domain separation tag
for intermediate Merkle tree nodes.
Rule 4. Nodes with Single Child¶
If height > 1, node T(height - 1, index * 2) exists and
node (height - 1, index * 2 + 1) is absent in the tree, then
T(height, index) = hash(
HashTag::ListBranchNode ||
T(height - 1, index * 2)
).
Getting Root Hash¶
root_hash = T(max_height, 0),
where max_height is the tree height as defined previously.
Merkle Tree Proofs¶
Proofs allow to efficiently and compactly verify that one or more elements are present at specific indexes in a Merkelized list. The proof also commits to the list length, so that it can be used to prove that the list does not contain elements with certain indexes.
One could think of proofs as of Merkle trees pruning. That is, a proof is produced by “collapsing” some intermediate nodes in the Merkle tree. Another point of view – from the light client perspective – is that a proof is essentially a limited view of a list, for which the Merkle tree is constructed. This view allows to calculate the hash of the whole list and proves that specific elements are present in the list.
Format¶
The proofs returned by the Exonum storage engine are non-recursive, thus minimizing overhead (e.g., heap allocations) and allowing to use them in environments not allowing recursive data types. A proof consists of three principal parts:
- Entries proven to exist in the list (i.e., values together with their indexes)
- Intermediate tree nodes (i.e.,
T(height, ..)values atheight > 0) that together with entries allow to restoreroot_hashof the Merkle tree for the list - List length
Entries and/or intermediate tree nodes may be empty.
Protobuf spec
message ListProof {
repeated HashedEntry proof = 1;
repeated ListProofEntry entries = 2;
uint64 length = 3;
}
// Represents list key and corresponding hash value.
message HashedEntry {
ProofListKey key = 1;
exonum.crypto.Hash hash = 2;
}
// Index of the list element and its value.
message ListProofEntry {
uint64 index = 1;
bytes value = 2;
}
// Represents list node position in the merkle tree.
message ProofListKey {
uint64 index = 1;
uint32 height = 2;
}
TypeScript spec of JSON serialization
interface ListProof<V> {
proof: HashedEntry[],
// first element in a tuple is element index,
// the second one is the JSON-serialized value
entries: [number, V][],
length: number,
}
interface HashedEntry {
height: number,
index: number,
hash: string, // 64 hex digits
}
Proof Verification¶
While validating the proof, a client restores root_hash and
computes the list hash. Depending on the use case, the list hash
can be compared to a trusted reference or participate in further aggregation.
Restoring root_hash can be performed as per above section:
- Compute
T(height = 1, ..)for entries according to rule 2. Letlayerdenote the obtained values. - Compute Merkle tree height
max_heightgiven length of the list. - For
height = 1, 2, ..., max_height - 1perform steps 4–5. - Combine
layerwith intermediate tree nodes from the proof at the same height into a single list,combined_layer. - “Lift” the nodes in
combined_layerto the next height according to rules 3 and 4. Assignlayerto be the resulting list. root_hash = layer[0]. At this point,layermust contain exactly one item.
To make the above procedure more effective, the proofs returned by MerkleDB
have entries ordered by increasing index and intermediate nodes ordered by
increasing (height, index) tuple. This allows to combine layers on step 4
and lift them on step 5 more effectively. If the client wants to take
the ordering into account during verification, the client must check it
in advance (which takes linear time w.r.t. the proof size).
See Also¶
- Merkle, R. C. — A Digital Signature Based on a Conventional Encryption Function // Advances in Cryptology — CRYPTO ’87. Lecture Notes in Computer Science, Vol. 293, pp. 369-378, 1988.
- Szydlo, M. — Merkle Tree Traversal in Log Space and Time // Lecture Notes in Computer Science, Vol. 3027, pp. 541-554, 2004.
- Merkle tree on Brilliant.